No edit summary Tag: Source edit |
Tag: Visual edit |
||
| (27 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
== '''Large Numbers''' == |
== '''Large Numbers''' == |
||
[[File:Big-number-table-explain--scaled.jpg|thumb|518x518px|Figure 1. Large numbers in modern Chinese]] |
[[File:Big-number-table-explain--scaled.jpg|thumb|518x518px|Figure 1. Large numbers in modern Chinese]] |
||
| + | Of all the excavated oracle bone inscriptions, 30000 was the largest number recorded by Shang dynasty scribes. It is clear that larger numbers were already in use by the Western Zhou dynasty (1046 - 771 BC). A poem from the ''Shijing'' (詩經, "Book of Odes") makes mention of the number of grain harvested on a good year: |
||
| + | {| class="fandom-table" |
||
| + | |'''周頌·豐年''' |
||
| + | 豐年多黍多稌, |
||
| + | |||
| + | 亦有高廩, |
||
| + | |||
| + | 萬億及秭。 |
||
| + | |||
| + | 為酒為醴, |
||
| + | |||
| + | 烝畀祖妣, |
||
| + | |||
| + | 以洽百禮, |
||
| + | |||
| + | 降福孔皆。 |
||
| + | |'''Eulogies of Zhou – Bumper Harvest''' |
||
| + | |||
| + | A year with abundant millet and rice, |
||
| + | |||
| + | We have our granaries high, |
||
| + | |||
| + | With billions of grain inside them. |
||
| + | |||
| + | We made spirits and sweet wine, |
||
| + | |||
| + | To offer our ancestors, |
||
| + | |||
| + | We complete the rituals, |
||
| + | |||
| + | May blessings be upon us all. |
||
| + | |} |
||
<br /> |
<br /> |
||
| + | Here, the character 秭 ''zi'' is equivalent to 萬億 ''wan yi.'' And since in this period of antiquity, 萬 ''wan'' meant ten-thousand (10<sup>4</sup>) and 億 ''yi'' meant hundred-thousand (10<sup>5</sup>); the character 秭 ''zi'' must be one billion (10<sup>9</sup>). Prior to the Han dynasty, the Chinese kept this rule of expressing large numbers as increasing powers of ten. After the Han Dynasty, there were other rules for expressing large numbers. According to the ''Sunzi Suanjing'', a text dated to between the 3<sup>rd</sup> and 5<sup>th</sup> centuries AD, large numbers increased by powers of ten-thousand or one-myriad (万 ''wan''). |
||
| + | {| class="fandom-table" |
||
| + | |凡大數之法,萬萬曰億,萬萬億曰兆,萬萬兆曰京,萬萬京曰垓,萬萬垓曰秭,萬萬秭曰壤,萬萬壤曰溝,萬萬溝曰澗,萬萬澗日正,萬萬正曰載。 |
||
| + | |The rule of large numbers states: ''wan-wan'' is called ''yi'' (億), ''wan-wan-yi'' is called ''zhao'' (兆), ''wan-wan-zhao'' is called ''jing'' (京), ''wan-wan-jing'' is called ''gai'' (垓), ''wan-wan-gai'' is called ''zi'' (秭), ''wan-wan-zi'' is called ''rang'' (壤), ''wan-wan-rang'' is called ''gou'' (溝), ''wan-wan-gou'' is ''jian'' (澗), ''wan-wan-jian'' is called ''zheng'' (正), ''wan-wan-zheng'' is called ''zai'' (載). |
||
| + | |} |
||
| + | <br /> |
||
| + | '''Table 1. Large numbers in the ''Sunzi Suanjing'' (3rd - 5th century AD)''' |
||
| + | {| class="fandom-table" |
||
| + | |'''Number''' |
||
| + | |'''Description in the ''Sunzi Suanjing''''' |
||
| + | |'''Value in the ''Sunzi Suanjing''''' |
||
| + | |- |
||
| + | |萬 ''wan'' |
||
| + | |10<sup>4</sup> |
||
| + | |10<sup>4</sup> |
||
| + | |- |
||
| + | |億 ''yi'' |
||
| + | |10<sup>4</sup>10<sup>4</sup> |
||
| + | |10<sup>8</sup> |
||
| + | |- |
||
| + | |兆 ''zhao'' |
||
| + | |10<sup>4</sup>10<sup>4</sup>10<sup>8</sup> |
||
| + | |10<sup>16</sup> |
||
| + | |- |
||
| + | |京 ''jing'' |
||
| + | |10<sup>4</sup>10<sup>4</sup>10<sup>16</sup> |
||
| + | |10<sup>24</sup> |
||
| + | |- |
||
| + | |垓 ''gai'' |
||
| + | |10<sup>4</sup>10<sup>4</sup>10<sup>24</sup> |
||
| + | |10<sup>32</sup> |
||
| + | |- |
||
| + | |秭 ''zi'' |
||
| + | |10<sup>4</sup>10<sup>4</sup>10<sup>32</sup> |
||
| + | |10<sup>40</sup> |
||
| + | |- |
||
| + | |壤 ''rang'' |
||
| + | |10<sup>4</sup>10<sup>4</sup>10<sup>40</sup> |
||
| + | |10<sup>48</sup> |
||
| + | |- |
||
| + | |溝 ''gou'' |
||
| + | |10<sup>4</sup>10<sup>4</sup>10<sup>48</sup> |
||
| + | |10<sup>56</sup> |
||
| + | |- |
||
| + | |澗 ''jian'' |
||
| + | |10<sup>4</sup>10<sup>4</sup>10<sup>56</sup> |
||
| + | |10<sup>64</sup> |
||
| + | |- |
||
| + | |正 ''zheng'' |
||
| + | |10<sup>4</sup>10<sup>4</sup>10<sup>64</sup> |
||
| + | |10<sup>72</sup> |
||
| + | |- |
||
| + | |載 ''zai'' |
||
| + | |10<sup>4</sup>10<sup>4</sup>10<sup>72</sup> |
||
| + | |10<sup>80</sup> |
||
| + | |} |
||
| + | Another description of large numbers can be found in an earlier mathematics called the ''Shushu Jiyi'' (數術記遺, "Memoir on the Methods of Numbering"). This text was written by the mathematician Xu Yue (徐岳, c. 180 - 220 AD) of the Eastern Han dynasty. In the ''Shushu Jiyi'', the same large numbers mentioned in the ''Sunzi Suanjing'' possess three "degrees" (等 ''deng''): "lower degree" (下等 ''xia deng'' or 下數 ''xia shu''), "medium degree" (中等 ''zhong deng'' or 中數 ''xia shu''), and "higher degree" (上等 ''shang deng'' or 上數 ''xia shu''). Note that the term “degree” (等 ''deng'') is used twice under different contexts. The first context, called the “ten degrees” (十等 ''shi deng''), signify the names of progressively large numbers; while the second context, called the “three degrees” (三等 ''san deng'') are the three categories of exponentiation. |
||
| − | == '''Minute Numbers''' == |
||
| + | {| class="fandom-table" |
||
| + | |黃帝為法,數有十等。 及其用也,乃有三焉。 十等者,億、兆,京、垓、秭、壤、溝、澗、正、載。 三等著,謂上、中、下也。 其下數者。 十十變之,若言十萬曰億,十億曰兆,十兆曰京也。 中數者,萬萬變之,若言萬萬曰億、萬萬億曰兆,萬萬兆曰京。 上數者,數窮則變,若言萬萬曰億,億億曰兆,兆兆曰京也。 |
||
| + | |In the method produced by the Yellow Emperor, numbers have ten degrees (十等 ''shi deng''). In practice [these ten degrees] are used in three ways. The ten degrees are ''yi'' (億), ''zhao'' (兆), ''jing'' (京), ''gai'' (垓), ''zi'' (秭), ''rang'' (壤), ''gou'' (溝), ''jian'' (澗), ''zheng'' (正), and ''zai'' (載). The “three degrees” (三等 ''san deng'') are the higher, the medium, and the lower. According to the lower degree, the numbers change by [a factor of] ten; for example, ten ''wan'' is called ''yi'', ten ''yi'' is called ''zhao'' and ten ''zhao'' is called ''jing''. According to the medium degree, the numbers change by [a factor of] myriad (万 ''wan''); for example, ''wan-wan'' is called ''yi'', a ''wan-wan-yi'' is called ''zhao'', and ''wan-wan-zhao'' is called ''jing''. According to the higher degree, the numbers change when available numbers are exhausted; for example, ''wan-wan'' is called ''yi'', ''yi-yi'' is called ''zhao'' and ''zhao-zhao'' is called ''jing''. |
||
| + | |} |
||
| + | <br /> |
||
| + | |||
| + | '''Table 2. Large numbers according to the rule as described in the ''Shushu Jiyi'' (3rd century AD)''' |
||
| + | {| class="fandom-table" |
||
| + | |'''Number''' |
||
| + | |'''Lower degree''' |
||
| + | |||
| + | 下等 |
||
| + | |'''Medium degree''' |
||
| + | |||
| + | 中等 |
||
| + | |'''Higher degree''' |
||
| + | |||
| + | 上等 |
||
| + | |- |
||
| + | |萬 ''wan'' |
||
| + | |10<sup>4</sup> |
||
| + | |10<sup>4</sup> |
||
| + | |10<sup>4</sup> |
||
| + | |- |
||
| + | |億 ''yi'' |
||
| + | |10<sup>5</sup> |
||
| + | |10<sup>8</sup> |
||
| + | |10<sup>8</sup> |
||
| + | |- |
||
| + | |兆 ''zhao'' |
||
| + | |10<sup>6</sup> |
||
| + | |10<sup>16</sup> |
||
| + | |10<sup>16</sup> |
||
| + | |- |
||
| + | |京 ''jing'' |
||
| + | |10<sup>7</sup> |
||
| + | |10<sup>24</sup> |
||
| + | |10<sup>32</sup> |
||
| + | |- |
||
| + | |垓 ''gai'' |
||
| + | |10<sup>8</sup> |
||
| + | |10<sup>32</sup> |
||
| + | |10<sup>64</sup> |
||
| + | |- |
||
| + | |秭 ''zi'' |
||
| + | |10<sup>9</sup> |
||
| + | |10<sup>40</sup> |
||
| + | |10<sup>128</sup> |
||
| + | |- |
||
| + | |壤 ''rang'' |
||
| + | |10<sup>10</sup> |
||
| + | |10<sup>48</sup> |
||
| + | |10<sup>256</sup> |
||
| + | |- |
||
| + | |溝 ''gou'' |
||
| + | |10<sup>11</sup> |
||
| + | |10<sup>56</sup> |
||
| + | |10<sup>512</sup> |
||
| + | |- |
||
| + | |澗 ''jian'' |
||
| + | |10<sup>12</sup> |
||
| + | |10<sup>64</sup> |
||
| + | |10<sup>1024</sup> |
||
| + | |- |
||
| + | |正 ''zheng'' |
||
| + | |10<sup>13</sup> |
||
| + | |10<sup>72</sup> |
||
| + | |10<sup>2048</sup> |
||
| + | |- |
||
| + | |載 ''zai'' |
||
| + | |10<sup>14</sup> |
||
| + | |10<sup>80</sup> |
||
| + | |10<sup>4096</sup> |
||
| + | |} |
||
| + | <br /> |
||
| + | From the description in the ''Shushu Jiyi'', it is clear that the traditional Zhou dynasty rule of increasing powers of ten became the "lower degree". The fact that the "middle degree" was retained in the ''Sunzi Suanjing'' verifies that it became the mathematical standard after the Han dynasty. |
||
| + | |||
| + | In later dynasties, there exists examples of large numbers named after Buddhist terminology. It is known that the mathematics and astronomy developed in India between the 5th to 7th centuries AD had made its way to China during the Sui and Tang dynasties. In consequence, many Indian concepts in philosophy, mythology, and religion (especially Buddhism) entered the Chinese vocabulary. In the ''Suanxue Qimeng'' (算學啟蒙, "Introduction to Mathematics"), a 13<sup>th</sup> century work by the mathematician Zhu Shijie (朱世杰, 1249–1314 AD), large numbers such as 恒河沙 (''heng he sha'', "sands in the Ganges") for 10<sup>96</sup>, 阿僧祇 (''a seng qi'', from Sanskrit "asaṅkhya" for "innumerable") for 10<sup>104</sup>, 那由他 (''na you ta'', from Sanskrit "niyuta" or "nayuta") for 10<sup>112</sup>, are clearly of foreign origin. |
||
| + | |||
| + | ==='''Problem Study 1: Nine Dykes'''=== |
||
| + | {| class="fandom-table" |
||
| + | |'''《孫子算經·卷下·34問》''' |
||
| + | 今有出門望見九隄。隄有九木,木有九枝,枝有九巢,巢有九禽,禽有九雛,雛有九毛,毛有九色。問:各幾何? |
||
| + | |||
| + | |||
| + | 答曰:木八十一。枝七百二十九。巢六千五百六十一。禽五萬九千四十九。雛五十三萬一千四百四十一。毛四百七十八萬二千九百六十九。色四千三百四萬六千七百二十一。 |
||
| + | |||
| + | |||
| + | 術曰:置九隄,以九乘之,得木之數。又以九乘之,得枝之數。又以九乘之,得巢之數。又以九乘之,得禽之數。又以九乘之,得雛之數。又以九乘之,得毛之敷。又以九乘之,得色之數。<br /> |
||
| + | |'''''Sunzi Suanjing'' (Chapter 3, Problem 34)''' |
||
| + | Suppose that after leaving a town gate, one sees 9 dykes. There are 9 trees on each dike, 9 branches on each tree, 9 nests on each branch, 9 birds in each nest, 9 fledglings per bird, 9 feathers on each fledgling, and 9 [different] colours on each feather. Question: How many are there of each? |
||
| + | |||
| + | |||
| + | |||
| + | Answer: 81 trees, 729 branches, 6,561 nests, 59,049 birds, 531,441 fledglings, 4,782,969 feathers, 43,046,721 colours. |
||
| + | |||
| + | |||
| + | Method: Set 9 dikes, multiply by 9 to obtain the number of trees. Next multiply by 9 to obtain the number of branches. Next multiply by 9 to obtain the number of nests. Next multiply by 9 to obtain the number of birds. Next multiply by 9 to obtain the number of fledglings. Next multiply by 9 to obtain the number of feathers. Next multiply by 9 to obtain the number of colours. |
||
| + | |} |
||
| + | <br /> |
||
| + | '''Solution to ''Sunzi Suanjing'' (Chapter 3, Problem 34)''' |
||
| + | |||
| + | {| class="fandom-table" |
||
| + | |<math> 9 \times 9 = 81 </math> |
||
| + | |81 trees |
||
| + | |- |
||
| + | |<math> 81 \times 9 = 729 </math> |
||
| + | |729 branches |
||
| + | |- |
||
| + | |<math> 729 \times 9 = 6561 </math> |
||
| + | |6561 nests |
||
| + | |- |
||
| + | |<math> 6561 \times 9 = 59059 </math> |
||
| + | |59049 birds |
||
| + | |- |
||
| + | |<math> 59059 \times 9 = 531441 </math> |
||
| + | |531441 fledglings |
||
| + | |- |
||
| + | |<math> 531441 \times 9 = 4782969 </math> |
||
| + | |4782969 feathers |
||
| + | |- |
||
| + | |<math> 4782969 \times 9 = 43046721 </math> |
||
| + | |43046721 colours |
||
| + | |} |
||
| + | |||
| + | ==='''Problem Study 2: Configurations on a Go Board'''=== |
||
| + | [[File:Go set.jpg|thumb|180x180px|Figure 2. Weiqi board with black and white stones.]] |
||
| + | An application of large numbers appears in one excerpt from the ''Mengxi Bitan'' (夢溪筆談, ''Brush Talks from Dream Brook'') by Shen Kuo (沈括, 960 - 1127 AD). Shen Kuo was a Song dynasty bureaucrat and polymath who wrote extensively on scientific topics. Here, Shen Kuo solves a combinatorial problem attributed to the Buddhist monk, astronomer, and inventor Yi Xing (一行, 673 – 727 AD). The problem asks for the number of configurations on a ''Weiqi'' board (in English, it is commonly called by its Japanese name Go), which led him to calculate the enormous number <math> {3}^{361} </math>. Shen Kuo made a few errors were made along the way; however, he did manage to obtain the correct order of magnitude! |
||
| + | <br /> |
||
| + | {| class="article-table" |
||
| + | |'''《夢溪筆談·卷18技藝7》''' |
||
| + | 小說:唐僧一行[1]曾算棋局都數,凡若干局盡之。 予嘗思之,此固易耳,但數多,非世間名數可能言之。 |
||
| + | |||
| + | 今略舉大數:凡方二路,用四子,可變八十一局; 方三路,用九子,可變一萬九千六百八十三局; 方四路,用十六子,可變四千三百四萬六千七百二十一局; 方五路,用二十五子,可變八千四百七十二億八千八百六十萬九千四百四十三局; 【古法:十萬為億,十億為兆,萬兆為稊[2]。 算家以萬萬為億,萬萬億為兆,萬萬兆為垓。 今但以算家數計之。】 方六路,用三十六子,可變十五兆九十四萬六千三百五十二億八千二百三萬一千九百二十六局[3]; 方七路以上,數多無名可記。 盡三百六十一路,大約連書萬字四十三,即是局之大數[4]。 【萬字四十三,最下萬字即萬局,第二是萬萬局,第三是萬億局,第四是一兆局,第五是萬兆局,第六是萬萬兆,謂之一垓,第七是萬垓局,第八是萬萬垓,第九是萬億萬萬垓。此外無名可紀,但四十三次萬倍乘之,即是都大數,零中數不與。】 |
||
| + | |||
| + | 其法:初一路可變三局。 【一黑、一白、一空。】 自後不以橫直,但增一子,即三因之。 凡三百六十一增,皆三因之,即是都局數。 |
||
| + | |||
| + | 又法:先計循邊一行為“法”,【凡十九路,得一十億六千二百二十六萬一千四百六十七局。】 凡加一行,即以“法”累乘之,乘終十九行,亦得上數。 |
||
| + | |||
| + | |||
| + | 又法:以自“法”相乘【得一百三十五兆八百五十一萬七千一百七十四億四千八百二十八萬七千三百三十四局,此是兩行,凡三十八路變得此數也。】 [5]下位副置之,以下乘上,又以下乘下,置為上位; 又副置之,以下乘上,以下乘下; 加一“法”,亦得上數。 有數法可求,唯此法最徑捷。 【只五次乘,便盡三百六十一路。】 千變萬化,不出此數,棋之局盡矣。 |
||
| + | |'''''Mengxi Bitan'' (Chapter 18 Jiyi 7)''' |
||
| + | |||
| + | According to a story, the Buddhist monk Yi Xing of the Tang dynasty calculated the total number of different configurations that may be placed on a Go board. I have thought of the problem as well, and found the method of calculation rather straightforward. However, the number of configurations is so large that it cannot be properly expressed by the numbers that are commonly known. |
||
| + | |||
| + | Here I shall present some examples. If the board is a 2x2 square grid, then it has four positions, which can produce 81 different configurations. If the board is a 3x3 square grid, then it has nine positions, which can produce 19,683 different configurations. If the board is a 4x4 square grid, then it has sixteen positions, which can produce 43,046,721 different configurations. If the board is a 5x5 square grid, then it has twenty-five positions, which can produce 847,288,609,443 different configurations. '''(According to the ancient number system: ''yi'' is 10 multiplied by 10,000, ''zhao'' is 10 multiplied by 100,000,000, ''ti''<sup>[2]</sup> is 10,000 multiplied by ''zhao''. However, for mathematicians, ''yi'' is 10000 multiplied by 10,000, ''zhao'' is 10,000 multiplied by 10,000 ''yi'', and ''gai'' is 10,000 multiplied by 10,000 ''zhao''. Here we use the calculation method of the mathematicians.)''' If the board is 6x6 square grid, then it has thirty-six positions, which can produce 150,094,635,282,031,926<sup>[3]</sup> different configurations. If the board is a 7x7 square grid or larger, the number of different configurations is too large to be written out. Exhausting the 361 positions of a true Go board, the number of configurations is approximately the number 10,000 being written consecutively forty-three times<sup>[4]</sup>. |
||
| + | |||
| + | '''(This so-called “forty-three 10,000s” means the last 10,000 is 10,000, the second is 10<sup>8</sup>, the third is 10<sup>12</sup>, the fourth is 10<sup>16</sup>, the fifth is 10<sup>20</sup>, the sixth is 10<sup>24</sup>, which is called one ''hai'', the seventh is 10<sup>28</sup>, the eighth is 10<sup>32</sup>, the ninth is 10<sup>36</sup>.''' '''Beyond that there is no name to express it; however, the product of 10000 to the power of 43 is the approximate order of magnitude of this large number while the remaining digits are not included.)''' |
||
| + | |||
| + | The method: first consider a point, which can have three possible configurations. '''(Black, white, or empty.)''' Each additional position, regardless if it is horizontal or vertical, will contribute an additional multiple of 3. When this is increased to 361 points, the total number of configurations is obtained by a multiple of 3 for every point. |
||
| + | |||
| + | Another method: First calculate the number of configurations of one side and take it as the “base number” (法 ''fa''). ('''There are 19 points in one line, so the number of configurations is 1,162,261,467.)''' If one more line is added to it, multiply it by the “base number”. When it is multiplied 19 times, we get the same number. |
||
| + | |||
| + | Another method: First multiply the “base number” by itself. '''(The product is 1,350,851,717,448,287,334<sup>[5]</sup>, which is the number of configurations for two lines with a total of 38 positions.)''' Then use the product as the multiplier and multiply the “base number” by the multiplier, and get the second result. After that, multiply the second product by itself and get the third product. Next use the third product as the multiplier and multiply it with the second product to get the fourth product. The total number of configurations is obtained after multiplying the product by itself and then multiplying it with the “base number”. Among these methods, this one is the quickest. '''(Only five calculations were made to arrive at the answer for 361 points.)''' Of all the myriad changes, the total number of configurations on a ''weiqi'' board will never exceed this number. This is indeed the final answer. |
||
| + | |} |
||
| + | <br /> |
||
| + | '''Notes''' |
||
| + | |||
| + | [1] Yi Xing, original name Zhang Sui (张遂, 673 – 727 AD), was an astronomer, mathematician, inventor and Buddhist monk of the Tang Dynasty. |
||
| + | |||
| + | [2] The character 稊 ''ti'' is a typographical error that should be written as 秭 ''zi''. |
||
| + | |||
| + | [3] The correct number should be 150,094,635,296,999,121. |
||
| + | |||
| + | [4] Shen Kuo gave the value 10<sup>172</sup>; however, the more precise value is 1.7409 x 10<sup>172</sup>. |
||
| + | |||
| + | [5] The correct number should be 1,350,851,717,672,992,089. |
||
| + | <br> |
||
| + | =='''Decimal Numbers'''== |
||
| + | On the opposite side of the spectrum are small numbers. Traditionally, small numbers were called "minute numbers" (微數 ''wei shu'') in China. Under closer inspection the "minute numbers" are expressed as decimal fractions denoted using Chinese characters that are associated with small linear measures after each digit to indicate the place value. In the ancient Chinese decimal system, each power of ten was represented by a specific character (Table 3). |
||
| + | |||
| + | '''Table 3. Minute numbers''' |
||
| + | {| class="fandom-table" |
||
| + | |- |
||
| + | |分 ''fen'' |
||
| + | |10<sup>-1</sup> |
||
| + | |- |
||
| + | |厘 ''li'' |
||
| + | |10<sup>-2</sup> |
||
| + | |- |
||
| + | |毫 ''hao'' |
||
| + | |10<sup>-3</sup> |
||
| + | |- |
||
| + | |秒 ''miao'' |
||
| + | |10<sup>-4</sup> |
||
| + | |- |
||
| + | |忽 ''hu'' |
||
| + | |10<sup>-5</sup> |
||
| + | |- |
||
| + | |微 ''wei'' |
||
| + | |10<sup>-6</sup> |
||
| + | |} |
||
| + | <br /> |
||
| + | According to the ''Sunzi Suanjing'', the terms ''hu'' (忽), ''miao'' (秒), ''hao'' (毫), ''li'' (厘), ''fen'' (分) are measurements of length, with ''hu'' (忽) being the smallest unit of length. Interestingly, the character ''hu'' (忽) derives its meaning from the width of silk threads woven by silkworms. Variations of this system of small numbers existed in later dynasties. In some cases, the ''miao'' 秒 is replaced with ''si'' 丝, another term for silk. Even smaller denominations such as ''wei'' (微), ''xian'' (纖), ''sha'' (沙) were included in later texts. |
||
| + | |||
| + | A good example of how ''minute numbers'' were used can be found in a passage of the ''Suishu'' (隋書, "Book of Sui"), which gives an account on Zu Chongzhi's value of π being between the deficit value (朒數, ''nü shu'') 3.1415926 and the excess value (盈數, ''ying shu'') 3.1415927. |
||
| + | {| class="fandom-table" |
||
| + | |圓周盈數三丈一尺四寸一分五厘九毫二秒七忽,朒數三丈一尺四寸一分五厘九毫二秒六忽,正數在盈、朒二限之間。 |
||
| + | |The excess value of the circumference is 3 ''zhang'' 1 ''chi'' 4 ''cun'' 1 ''fen'' 5 ''li'' 9 ''hao'' 2 ''miao'' 7 ''hu'', and the deficit value is 3 ''zhang'' 1 ''chi'' 4 ''cun'' 1 ''fen'' 5 ''li'' 9 ''hao'' 2 ''miao'' 6 ''hu''. The actual number lies between the excess and deficit values.<br /> |
||
| + | |} |
||
| + | <br /> |
||
| + | |||
| + | [[Category:Chinese Mathematics]] |
||
| + | [[Category:Arithmetic and Conversions]] |
||
| + | [[Category:Science and Technology in East Asia]] |
||
Latest revision as of 15:38, 4 April 2022
By: Tao Steven Zheng (郑涛)
Large Numbers
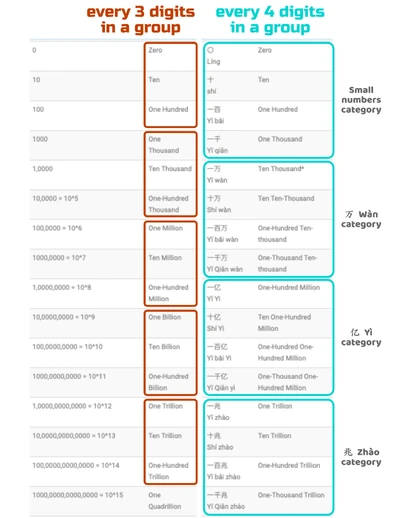
Figure 1. Large numbers in modern Chinese
Of all the excavated oracle bone inscriptions, 30000 was the largest number recorded by Shang dynasty scribes. It is clear that larger numbers were already in use by the Western Zhou dynasty (1046 - 771 BC). A poem from the Shijing (詩經, "Book of Odes") makes mention of the number of grain harvested on a good year:
| 周頌·豐年
豐年多黍多稌, 亦有高廩, 萬億及秭。 為酒為醴, 烝畀祖妣, 以洽百禮, 降福孔皆。 |
Eulogies of Zhou – Bumper Harvest
A year with abundant millet and rice, We have our granaries high, With billions of grain inside them. We made spirits and sweet wine, To offer our ancestors, We complete the rituals, May blessings be upon us all. |
Here, the character 秭 zi is equivalent to 萬億 wan yi. And since in this period of antiquity, 萬 wan meant ten-thousand (104) and 億 yi meant hundred-thousand (105); the character 秭 zi must be one billion (109). Prior to the Han dynasty, the Chinese kept this rule of expressing large numbers as increasing powers of ten. After the Han Dynasty, there were other rules for expressing large numbers. According to the Sunzi Suanjing, a text dated to between the 3rd and 5th centuries AD, large numbers increased by powers of ten-thousand or one-myriad (万 wan).
| 凡大數之法,萬萬曰億,萬萬億曰兆,萬萬兆曰京,萬萬京曰垓,萬萬垓曰秭,萬萬秭曰壤,萬萬壤曰溝,萬萬溝曰澗,萬萬澗日正,萬萬正曰載。 | The rule of large numbers states: wan-wan is called yi (億), wan-wan-yi is called zhao (兆), wan-wan-zhao is called jing (京), wan-wan-jing is called gai (垓), wan-wan-gai is called zi (秭), wan-wan-zi is called rang (壤), wan-wan-rang is called gou (溝), wan-wan-gou is jian (澗), wan-wan-jian is called zheng (正), wan-wan-zheng is called zai (載). |
Table 1. Large numbers in the Sunzi Suanjing (3rd - 5th century AD)
| Number | Description in the Sunzi Suanjing | Value in the Sunzi Suanjing |
| 萬 wan | 104 | 104 |
| 億 yi | 104104 | 108 |
| 兆 zhao | 104104108 | 1016 |
| 京 jing | 1041041016 | 1024 |
| 垓 gai | 1041041024 | 1032 |
| 秭 zi | 1041041032 | 1040 |
| 壤 rang | 1041041040 | 1048 |
| 溝 gou | 1041041048 | 1056 |
| 澗 jian | 1041041056 | 1064 |
| 正 zheng | 1041041064 | 1072 |
| 載 zai | 1041041072 | 1080 |
Another description of large numbers can be found in an earlier mathematics called the Shushu Jiyi (數術記遺, "Memoir on the Methods of Numbering"). This text was written by the mathematician Xu Yue (徐岳, c. 180 - 220 AD) of the Eastern Han dynasty. In the Shushu Jiyi, the same large numbers mentioned in the Sunzi Suanjing possess three "degrees" (等 deng): "lower degree" (下等 xia deng or 下數 xia shu), "medium degree" (中等 zhong deng or 中數 xia shu), and "higher degree" (上等 shang deng or 上數 xia shu). Note that the term “degree” (等 deng) is used twice under different contexts. The first context, called the “ten degrees” (十等 shi deng), signify the names of progressively large numbers; while the second context, called the “three degrees” (三等 san deng) are the three categories of exponentiation.
| 黃帝為法,數有十等。 及其用也,乃有三焉。 十等者,億、兆,京、垓、秭、壤、溝、澗、正、載。 三等著,謂上、中、下也。 其下數者。 十十變之,若言十萬曰億,十億曰兆,十兆曰京也。 中數者,萬萬變之,若言萬萬曰億、萬萬億曰兆,萬萬兆曰京。 上數者,數窮則變,若言萬萬曰億,億億曰兆,兆兆曰京也。 | In the method produced by the Yellow Emperor, numbers have ten degrees (十等 shi deng). In practice [these ten degrees] are used in three ways. The ten degrees are yi (億), zhao (兆), jing (京), gai (垓), zi (秭), rang (壤), gou (溝), jian (澗), zheng (正), and zai (載). The “three degrees” (三等 san deng) are the higher, the medium, and the lower. According to the lower degree, the numbers change by [a factor of] ten; for example, ten wan is called yi, ten yi is called zhao and ten zhao is called jing. According to the medium degree, the numbers change by [a factor of] myriad (万 wan); for example, wan-wan is called yi, a wan-wan-yi is called zhao, and wan-wan-zhao is called jing. According to the higher degree, the numbers change when available numbers are exhausted; for example, wan-wan is called yi, yi-yi is called zhao and zhao-zhao is called jing. |
Table 2. Large numbers according to the rule as described in the Shushu Jiyi (3rd century AD)
| Number | Lower degree
下等 |
Medium degree
中等 |
Higher degree
上等 |
| 萬 wan | 104 | 104 | 104 |
| 億 yi | 105 | 108 | 108 |
| 兆 zhao | 106 | 1016 | 1016 |
| 京 jing | 107 | 1024 | 1032 |
| 垓 gai | 108 | 1032 | 1064 |
| 秭 zi | 109 | 1040 | 10128 |
| 壤 rang | 1010 | 1048 | 10256 |
| 溝 gou | 1011 | 1056 | 10512 |
| 澗 jian | 1012 | 1064 | 101024 |
| 正 zheng | 1013 | 1072 | 102048 |
| 載 zai | 1014 | 1080 | 104096 |
From the description in the Shushu Jiyi, it is clear that the traditional Zhou dynasty rule of increasing powers of ten became the "lower degree". The fact that the "middle degree" was retained in the Sunzi Suanjing verifies that it became the mathematical standard after the Han dynasty.
In later dynasties, there exists examples of large numbers named after Buddhist terminology. It is known that the mathematics and astronomy developed in India between the 5th to 7th centuries AD had made its way to China during the Sui and Tang dynasties. In consequence, many Indian concepts in philosophy, mythology, and religion (especially Buddhism) entered the Chinese vocabulary. In the Suanxue Qimeng (算學啟蒙, "Introduction to Mathematics"), a 13th century work by the mathematician Zhu Shijie (朱世杰, 1249–1314 AD), large numbers such as 恒河沙 (heng he sha, "sands in the Ganges") for 1096, 阿僧祇 (a seng qi, from Sanskrit "asaṅkhya" for "innumerable") for 10104, 那由他 (na you ta, from Sanskrit "niyuta" or "nayuta") for 10112, are clearly of foreign origin.
Problem Study 1: Nine Dykes
| 《孫子算經·卷下·34問》
今有出門望見九隄。隄有九木,木有九枝,枝有九巢,巢有九禽,禽有九雛,雛有九毛,毛有九色。問:各幾何?
|
Sunzi Suanjing (Chapter 3, Problem 34)
Suppose that after leaving a town gate, one sees 9 dykes. There are 9 trees on each dike, 9 branches on each tree, 9 nests on each branch, 9 birds in each nest, 9 fledglings per bird, 9 feathers on each fledgling, and 9 [different] colours on each feather. Question: How many are there of each?
Answer: 81 trees, 729 branches, 6,561 nests, 59,049 birds, 531,441 fledglings, 4,782,969 feathers, 43,046,721 colours.
|
Solution to Sunzi Suanjing (Chapter 3, Problem 34)
| 81 trees | |
| 729 branches | |
| 6561 nests | |
| 59049 birds | |
| 531441 fledglings | |
| 4782969 feathers | |
| 43046721 colours |
Problem Study 2: Configurations on a Go Board

Figure 2. Weiqi board with black and white stones.
An application of large numbers appears in one excerpt from the Mengxi Bitan (夢溪筆談, Brush Talks from Dream Brook) by Shen Kuo (沈括, 960 - 1127 AD). Shen Kuo was a Song dynasty bureaucrat and polymath who wrote extensively on scientific topics. Here, Shen Kuo solves a combinatorial problem attributed to the Buddhist monk, astronomer, and inventor Yi Xing (一行, 673 – 727 AD). The problem asks for the number of configurations on a Weiqi board (in English, it is commonly called by its Japanese name Go), which led him to calculate the enormous number . Shen Kuo made a few errors were made along the way; however, he did manage to obtain the correct order of magnitude!
| 《夢溪筆談·卷18技藝7》
小說:唐僧一行[1]曾算棋局都數,凡若干局盡之。 予嘗思之,此固易耳,但數多,非世間名數可能言之。 今略舉大數:凡方二路,用四子,可變八十一局; 方三路,用九子,可變一萬九千六百八十三局; 方四路,用十六子,可變四千三百四萬六千七百二十一局; 方五路,用二十五子,可變八千四百七十二億八千八百六十萬九千四百四十三局; 【古法:十萬為億,十億為兆,萬兆為稊[2]。 算家以萬萬為億,萬萬億為兆,萬萬兆為垓。 今但以算家數計之。】 方六路,用三十六子,可變十五兆九十四萬六千三百五十二億八千二百三萬一千九百二十六局[3]; 方七路以上,數多無名可記。 盡三百六十一路,大約連書萬字四十三,即是局之大數[4]。 【萬字四十三,最下萬字即萬局,第二是萬萬局,第三是萬億局,第四是一兆局,第五是萬兆局,第六是萬萬兆,謂之一垓,第七是萬垓局,第八是萬萬垓,第九是萬億萬萬垓。此外無名可紀,但四十三次萬倍乘之,即是都大數,零中數不與。】 其法:初一路可變三局。 【一黑、一白、一空。】 自後不以橫直,但增一子,即三因之。 凡三百六十一增,皆三因之,即是都局數。 又法:先計循邊一行為“法”,【凡十九路,得一十億六千二百二十六萬一千四百六十七局。】 凡加一行,即以“法”累乘之,乘終十九行,亦得上數。
|
Mengxi Bitan (Chapter 18 Jiyi 7)
According to a story, the Buddhist monk Yi Xing of the Tang dynasty calculated the total number of different configurations that may be placed on a Go board. I have thought of the problem as well, and found the method of calculation rather straightforward. However, the number of configurations is so large that it cannot be properly expressed by the numbers that are commonly known. Here I shall present some examples. If the board is a 2x2 square grid, then it has four positions, which can produce 81 different configurations. If the board is a 3x3 square grid, then it has nine positions, which can produce 19,683 different configurations. If the board is a 4x4 square grid, then it has sixteen positions, which can produce 43,046,721 different configurations. If the board is a 5x5 square grid, then it has twenty-five positions, which can produce 847,288,609,443 different configurations. (According to the ancient number system: yi is 10 multiplied by 10,000, zhao is 10 multiplied by 100,000,000, ti[2] is 10,000 multiplied by zhao. However, for mathematicians, yi is 10000 multiplied by 10,000, zhao is 10,000 multiplied by 10,000 yi, and gai is 10,000 multiplied by 10,000 zhao. Here we use the calculation method of the mathematicians.) If the board is 6x6 square grid, then it has thirty-six positions, which can produce 150,094,635,282,031,926[3] different configurations. If the board is a 7x7 square grid or larger, the number of different configurations is too large to be written out. Exhausting the 361 positions of a true Go board, the number of configurations is approximately the number 10,000 being written consecutively forty-three times[4]. (This so-called “forty-three 10,000s” means the last 10,000 is 10,000, the second is 108, the third is 1012, the fourth is 1016, the fifth is 1020, the sixth is 1024, which is called one hai, the seventh is 1028, the eighth is 1032, the ninth is 1036. Beyond that there is no name to express it; however, the product of 10000 to the power of 43 is the approximate order of magnitude of this large number while the remaining digits are not included.) The method: first consider a point, which can have three possible configurations. (Black, white, or empty.) Each additional position, regardless if it is horizontal or vertical, will contribute an additional multiple of 3. When this is increased to 361 points, the total number of configurations is obtained by a multiple of 3 for every point. Another method: First calculate the number of configurations of one side and take it as the “base number” (法 fa). (There are 19 points in one line, so the number of configurations is 1,162,261,467.) If one more line is added to it, multiply it by the “base number”. When it is multiplied 19 times, we get the same number. Another method: First multiply the “base number” by itself. (The product is 1,350,851,717,448,287,334[5], which is the number of configurations for two lines with a total of 38 positions.) Then use the product as the multiplier and multiply the “base number” by the multiplier, and get the second result. After that, multiply the second product by itself and get the third product. Next use the third product as the multiplier and multiply it with the second product to get the fourth product. The total number of configurations is obtained after multiplying the product by itself and then multiplying it with the “base number”. Among these methods, this one is the quickest. (Only five calculations were made to arrive at the answer for 361 points.) Of all the myriad changes, the total number of configurations on a weiqi board will never exceed this number. This is indeed the final answer. |
Notes
[1] Yi Xing, original name Zhang Sui (张遂, 673 – 727 AD), was an astronomer, mathematician, inventor and Buddhist monk of the Tang Dynasty.
[2] The character 稊 ti is a typographical error that should be written as 秭 zi.
[3] The correct number should be 150,094,635,296,999,121.
[4] Shen Kuo gave the value 10172; however, the more precise value is 1.7409 x 10172.
[5] The correct number should be 1,350,851,717,672,992,089.
Decimal Numbers
On the opposite side of the spectrum are small numbers. Traditionally, small numbers were called "minute numbers" (微數 wei shu) in China. Under closer inspection the "minute numbers" are expressed as decimal fractions denoted using Chinese characters that are associated with small linear measures after each digit to indicate the place value. In the ancient Chinese decimal system, each power of ten was represented by a specific character (Table 3).
Table 3. Minute numbers
| 分 fen | 10-1 |
| 厘 li | 10-2 |
| 毫 hao | 10-3 |
| 秒 miao | 10-4 |
| 忽 hu | 10-5 |
| 微 wei | 10-6 |
According to the Sunzi Suanjing, the terms hu (忽), miao (秒), hao (毫), li (厘), fen (分) are measurements of length, with hu (忽) being the smallest unit of length. Interestingly, the character hu (忽) derives its meaning from the width of silk threads woven by silkworms. Variations of this system of small numbers existed in later dynasties. In some cases, the miao 秒 is replaced with si 丝, another term for silk. Even smaller denominations such as wei (微), xian (纖), sha (沙) were included in later texts.
A good example of how minute numbers were used can be found in a passage of the Suishu (隋書, "Book of Sui"), which gives an account on Zu Chongzhi's value of π being between the deficit value (朒數, nü shu) 3.1415926 and the excess value (盈數, ying shu) 3.1415927.
| 圓周盈數三丈一尺四寸一分五厘九毫二秒七忽,朒數三丈一尺四寸一分五厘九毫二秒六忽,正數在盈、朒二限之間。 | The excess value of the circumference is 3 zhang 1 chi 4 cun 1 fen 5 li 9 hao 2 miao 7 hu, and the deficit value is 3 zhang 1 chi 4 cun 1 fen 5 li 9 hao 2 miao 6 hu. The actual number lies between the excess and deficit values. |








